First of all, I want to anounce that I have enabled comments in the blog, so readers can comment on the entries. Let’s see if this new feature enriches the blog.

After having some troubles to get them working, we have the first two nipype workflows running. Both are pairwise calculations made over a series of signals selected by the user with a mask:

• Pairwise Correlation over timeseries given a mask.
• Pairwise Mutual Information over timeseries given a mask.

1
2
3
4
5
6
7
8
9

def compute_ROI_corr(in_file, mask_file):

    from CPAC.series_mod import gen_roi_timeseries
    from CPAC.series_mod import corr

    ROI_data = gen_roi_timeseries(in_file, mask_file)
    corr_mat = corr(ROI_data)

    return corr_mat

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

def compute_MI(in_file, mask_file, bins):

    from CPAC.series_mod import gen_roi_timeseries
    from CPAC.series_mod import transform
    from CPAC.series_mod import mutual_information

    import numpy as np

    ROI_data = gen_roi_timeseries(in_file, mask_file)
    ROI_data = transform(ROI_data,bins).astype(int)

    n_var = ROI_data.shape[0];

    MI_mat = np.zeros((n_var,n_var))

    for i_ in range(n_var):
        for j_ in range(n_var):
            MI_mat[i_,j_] = mutual_information(ROI_data[i_,:],ROI_data[j_,:])

    return MI_mat

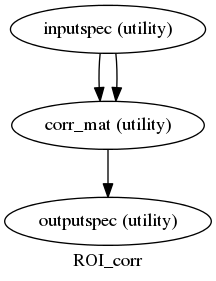
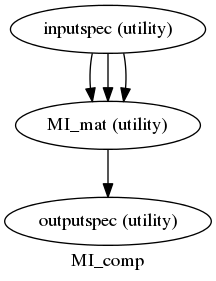
In both of them a fMRI file and a mask are needed, and for the MI calculation a variable “bins” is also needed. This variable is the number of states that the user wants the signals to be discretized to.

This brings up a new problem; how many states should we choose to discretize? We are working on this question and discussing whether we should introduce a measure that optimizes the number of bins/states to choose, between other fitting entropy or correlation formalisms. Seems like we could implement some tests to choose a proper “number of states”, we will have a further debate.

The discretization is done with the following helper function:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

def transform(x_old, Nbins):

    '''
    TRANSFORM This funcion computes transforms in a matrix
    to obtain a matrix scaled between the especified number of bins
    INPUT:
      x_old: nobservations * nvariables matrix
      Nbins: Number of bins of the transformed matrix (NBins=2 values betwen
     -1, NBins=3 values between 0-2...)

    OUTPUT:  
    x_new: New scaled matrix
    '''

    import numpy as np

    [npoints, num_vals] = x_old.shape
    xmax = Nbins-1
    xmin = 0
    ymax = x_old.max()
    ymin = x_old.min()

    #x_new = ((xmax - xmin)/(ymax - ymin) )* x_old - ( (xmax - xmin) / (ymax - ymin) ) * ymin + xmin;

    x = (xmax-xmin)/(ymax-ymin)
    x_new = x * x_old
    x_new = x_new - (x*ymin+xmin)
    x_new = np.round(x_new)

    return x_new

Also, when testing the workflows, we encountered another problem. While running the scripts by our own with the code alone, we had the results as we were expecting; but, when building and running the workflows, we can not get the results. We need to investigate on this, since is the basis of many things.

To do:

• Solve the problems with workflows.
• Try real data over the workflows and see if we can get some interesting results.
• Implement further synchronization analysis measures.